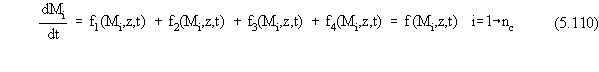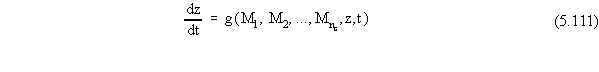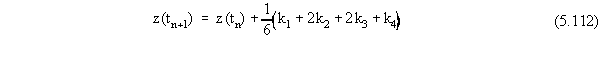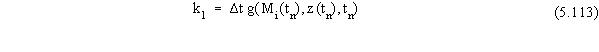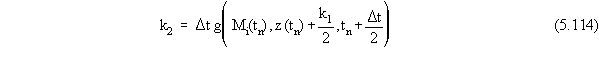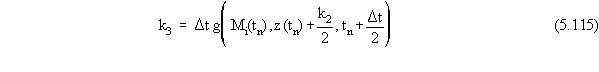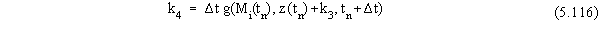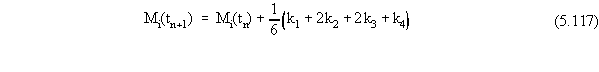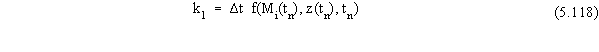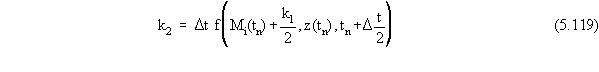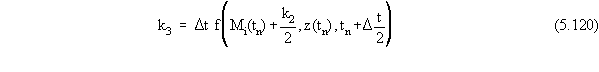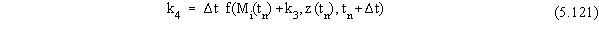5.7 Numerical Solution Procedure for the General Case

     In the general case of multiple, concurrent, contaminant loss pathways, an analytical solution to Equation 5.56 is not possible. Some of the reasons for this are the same as those discussed for the contaminated aquifer and contaminated pond source zones (i.e., complex NAPL partitioning theory, time varying parameters). When a NAPL phase is present in the source zone, the leaching term cannot be expressed as a single, simple function of M_i and t. Furthermore, even when a NAPL phase is not present, a number of system parameters may be arbitrary functions of time. In the case of the contaminated vadose zone source zone, the parameters that may be varying in time (due to natural phenomenon or the implementation of remediation methodologies ) include the Darcy water flux density, wind suspension rate, and water erosion rate. The user has the ability to enter these parameters as a time series of discrete values. There are no hard limits on the number of elements constituting the time series used to describe such parameters. The code will allocate available memory as it is needed. Therefore, any arbitrary Darcy water flux density, wind suspension rate, or water erosion rate can be accommodated, provide memory and run time limits are not exceeded. In addition, when the volatilization loss route is included, the mathematical problem consists of simultaneously solving a set of coupled differential equations (rather than just one differential equation in M_i): one set of equations for the masses of each contaminant (e.g., Equation 5.99), plus one more for the position of the top boundary of the source zone (e.g., Equation 5.101).

     In other words, the mathematical problem actually consists of the simultaneous numerical solution of a set of first-order, ordinary differential equations of the following form:





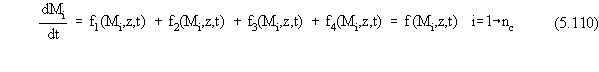
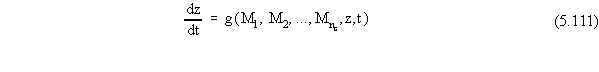
     where f₁(•), f₂(•), f₃(•), f₄(•), f(•), and g(•) are generic representations of functions of the variables M_i(t), z(t), and t. Furthermore, each of the four individual functions, f₁(•), f₂(•), f₃(•), and f4(•), in Equation 5.110 represent one of the individual mass loss flux terms. Note that in reality, the function f(•) in the specific Equation 5.110 that corresponds to contaminant i might only depend on the mass M_i, and not the other masses. However, in general it can be said that f(•) is a function of all of the masses, z, and t (and that the functional dependence on masses other than M_i is nil). Therefore, Equations 5.110 and 5.111 truly can be described as a set of n_c+1 first-order, ordinary differential equations in n_c+1 unknowns.

     The source-term release module solves this set of first-order, ordinary differential equations numerically by using a fourth-order Runge-Kutta method. This method requires four computations of the function f(•) or g(•) for each time step. The numerical algorithm begins at time t = 0 with M_i = M_io, and z = z_t. The value of z is updated first, using Equation 5.111 and assuming that the values of M_i for all the contaminants are held constant at their values at the beginning of the time step. Then each of the values of M_i are updated, using an equation like Equation 5.110 for each contaminant and assuming that the value of z is held constant at its value at the beginning of the time step.

     The Runge-Kutta algorithm for updating the position of the top boundary of the source zone over the course of a time step is given by



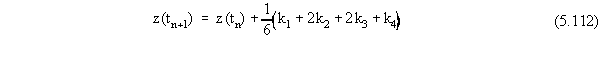
where the terms in Equation 5.112 are given by









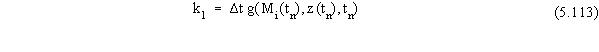
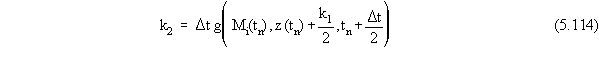
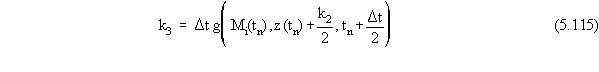
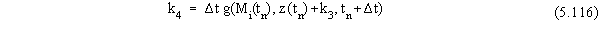
     (In the above equations, M_i(t_n) and z(t_n) are the values of M_i and z, respectively, at the time nDt; and t_n is the time nDt.) As long as a clean layer exists above the source zone, this numerical solution of Equation 5.111 is the appropriate way to update the value of z over the course of the time step. However, if wind suspension and water erosion would have caused the soil surface to recede to a depth deeper than this calculated value of z (from volatilization loss considerations) over the course of the time step, then z must be updated according to wind suspension and water erosion considerations. In other words, the value of z calculated from solution of Equation 5.111 must be compared to (S+E)t. If (S+E)t is the greater of these two quantities, the updated value of z is reset equal to (S+E)t.

      The Runge-Kutta algorithm for updating contaminant masses over the course of a time step is given by



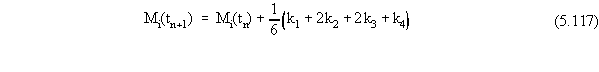
where the terms in Equation 5.117 are given by









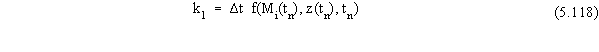
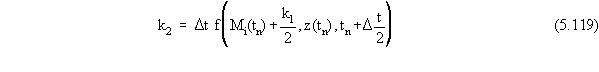
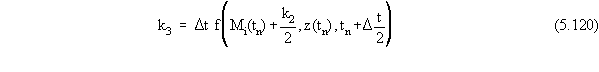
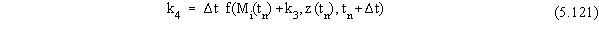
     Note that because the function f(•) can be expressed as the sum of the functions f₁(•), f₂(•), f₃(•), and f₄(•) (from Equation 5.110), the Runge-Kutta procedure used to update the total contaminant mass in the source zone (described in Equations 5.117 through 5.121) contains calculations of the k₁ through k₄ terms that would be associated with the individual functions f₁(•), f₂(•), f₃(•), and f₄(•). Because these functions are associated with the individual mass loss terms, the numerical scheme allows us to also obtain the individual mass fluxes to each loss route at discrete times with minimal extra computation. This entire procedure is repeated as long as not all of the contaminant mass has been depleted from the source zone.

---