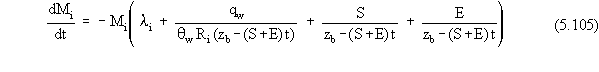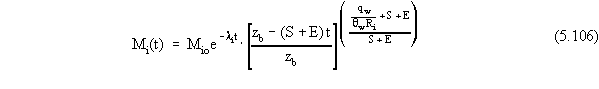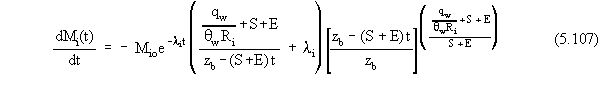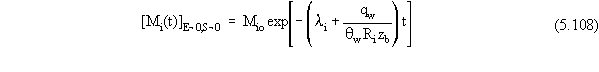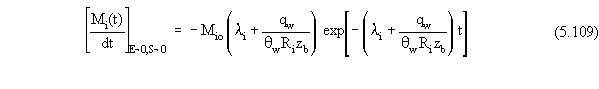5.6 Special Cases with Analytical Solutions

     For scenarios where a) no NAPL phase is present, b) no volatilization occurs, c) no clean layer of soil exists above the source zone, d) no contaminant decays into another contaminant, and e) no remediation methodologies that must be described by unique theory are implemented, the resulting overall mass flux equation (i.e., Equation 5.56) has an analytical solution. The mass flux terms for decay/degradation, leaching, wind suspension, and water erosion are given by Equations 5.57, 5.92, 5.97, and 5.98, respectively. If these terms are substituted into Equation 5.56, the mass flux equation for this special case of multiple concurrent loss pathways is



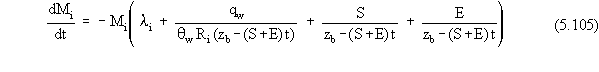
     The analytical solution to Equation 5.105, assuming that the initial mass (at t = 0) of contaminant i is M_io, is



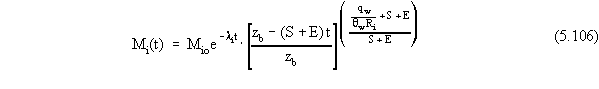
     This expression gives the total mass of a contaminant still within the source zone as a function time. Differentiating Equation 5.106 with respect to time (or substituting Equation 5.106 into Equation 5.105) gives



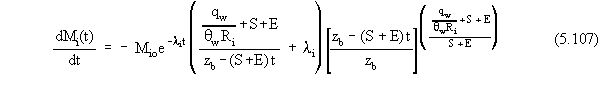
     which is an expression for the total mass flux lost from the source zone as a function of time. Equation 5.106 could be substituted into Equations 5.57, 5.92, 5.97, and 5.98 to produce analytical expressions for the individual mass loss rates as well. Equations 5.57, 5.92, 5.97, 5.98, and 5.106 could then be used to verify the outputs of the source-term release module for these scenarios, if none of the contaminants decay/degrade into other species of concern (e.g., other contaminants in the initial source inventory). If they do, this set of analytical solutions will not capture the entire decay-chain behavior (as the numerical procedure will).

      Simpler scenarios (i.e., ones in which only a subsets of these four mass loss processes are occurring) can be modeled by these same equations by simply allowing the parameters related to the absent processes to go to zero. This is just a straightforward task of substituting zero for l_i, q_w, S, or E for all scenarios except ones where both wind suspension and surface water erosion are absent. In this case, setting S and E to zero would cause the exponent in Equations 5.106 and 5.107 to approach infinity; and so the proper procedure is to take the limit of the right-hand side of Equation 5.106 as S and E approach zero to obtain the following expression:



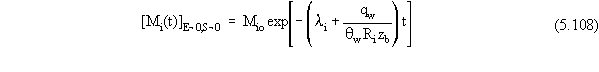
     When S and E are both zero, the total mass flux lost from the source zone as a function of time can be calculated by differentiating Equation 5.108 with respect to time to obtain



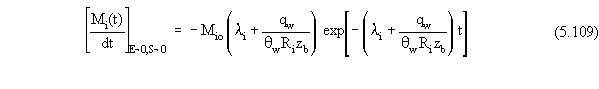
     Closed-form expressions for the mass fluxes to each loss pathway (for this special case) can be obtained by substituting Equation 5.109 into Equations 5.57 and 5.92.