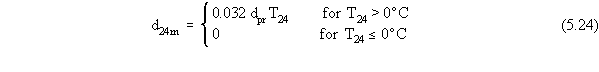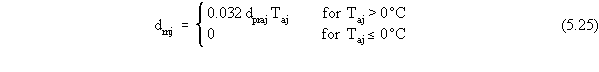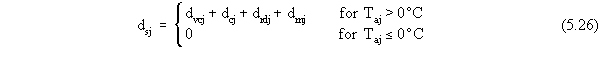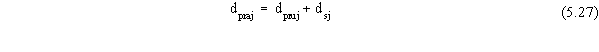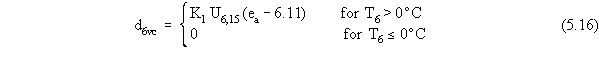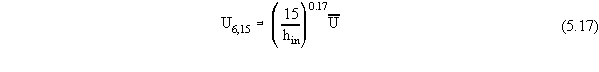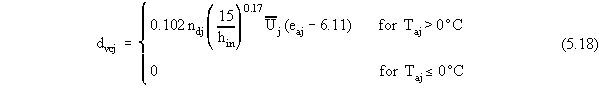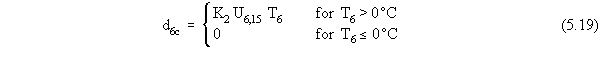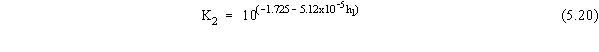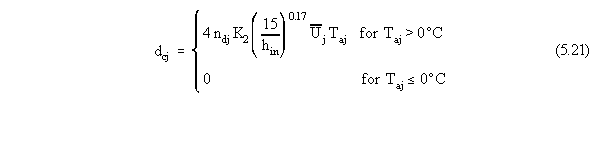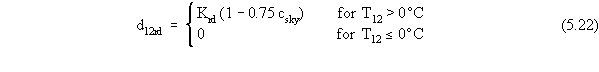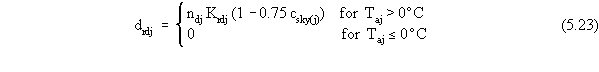5.1.4  Adjusted Precipitation

    The average monthly precipitation contained in the LCD is assumed to be rainfall if the adjusted average monthly temperature is above freezing, and snowfall if the temperature is below freezing.  This assumption is not completely accurate, because rainfall and snowfall frequently occur during the same month, especially during the springtime.  However, if the average temperature for the month is above freezing, much of the snowfall will melt and represent a source of water for percolation and overland runoff.

    The assumption used in this methodology is that snow is stored on the ground when the adjusted average temperature is less than or equal to 0^o C (32^o F).  When the temperature rises above freezing, the snow melts and is available for percolation and runoff.  Simple empirical relationships are used to estimate snowmelt.  Heat necessary to induce snowmelt is derived from radiation, condensation of vapor, convection, air and ground conduction, and rainfall.  The four most important sources are vapor condensation, convection, radiation, and rainfall.  Of these sources, vapor condensation is considered one of the most important factors, while rainfall ranks fourth as an important heat source (Linsley and Franzini 1972; Linsley et al. 1975; Viessman et al. 1977).  Each of these four sources is discussed below.

Vapor Condensation
    Viessman et al. (1977) note that heat given off by condensing water vapor in a snowpack is often the most important source of heat for snowmelt.  A water vapor supply at the snow surface is formed by the turbulent exchange process.  Consequently, a mass transfer equation similar to those presented for evaporation studies fits the melt process (Viessman et al. 1977).  An expression for a 6-hr depth of snowmelt is given as (Light 1941 as reported by Viessman et al. 1977)



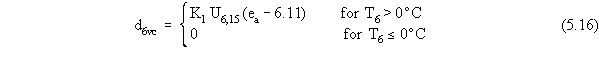
where

d_6vc is the 6-hr snowmelt from vapor condensation (cm)
K₁  is the theoretical constant in equation for snowmelt by vapor condensation  (cm s mbar^-1 m^-1)
U_6,15 is the average 6-hr wind velocity measured at 15 m (50 ft) above the ground (m s^-1)
e_a  is the actual vapor pressure of the air (mbar).

The value of K₁ reportedly varies from 0.01818 to 0.03284 (cm s mbar^-1 m^-1) [0.00320 to 0.00578 (hr in. mbar^-1 mi^-1)] (Light 1941 and Wilson 1941, as reported by Viessman et al. 1977).  An average value of 0.02557 (cm s mbar^-1 m^-1) [0.0045 (hr in. mbar^-1 mi^-1)] is chosen for K₁.  If the wind speed measurements were not made at 15 m (50 ft), then they can be calculated as follows



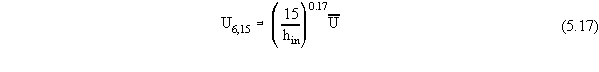
where    is the average wind speed (m s^-1).

Because available data are on a monthly basis, it is assumed that the 6-hr snowmelt computations can be extended over the month by using adjusted averaged monthly temperatures and wind speeds.  By assuming that no evaporation of snow occurs, the monthly estimate of depth of snowmelt from vapor condensation can be expressed as follows:



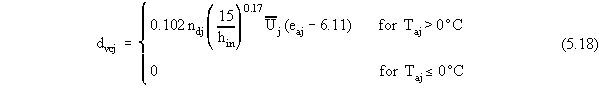
where

d_vcj    is the average monthly snowmelt from vapor condensation for the j-th month (cm)
n_dj       is the number of days in the j-th month (unitless).

The actual vapor pressure (e_aj) is estimated using Equations 5.9 and 5.10 of Section 5.1.3.2.

     Convection
Heat is transferred from the atmosphere to the snowpack by convection (Viessman et al. 1977).  The amount of snowmelt by this process is related to temperature and wind speed.  Wilson (1941) and Light (1941), as reported by Viessman et al. (1977), provide an expression for estimating the 6-hr depth of snowmelt by convection as


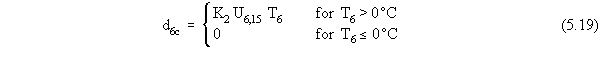
in which



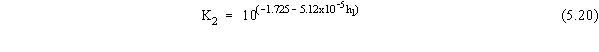
where

d_6c  is the 6-hr snowmelt from convection (cm)
K₂  is the heat exchange coefficient as a function of elevation  (cm s m^{-1  o}C^-1)
T₆  is the average 6-hr temperature (^oC).

It is assumed that the 6-hr snowmelt can be extended over the month by using adjusted averaged monthly temperatures and wind speeds.  The monthly estimate for snowmelt from convection is given by



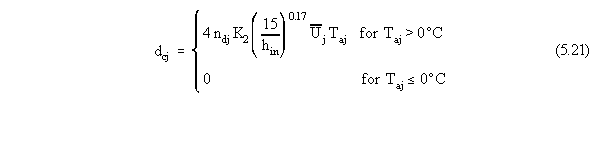
where   d_cj is the average monthly snowmelt from convection for the j-th month (cm).

Radiation

The net amount of shortwave and longwave radiation received by a snowpack can be a very important source of heat energy for snowmelt (Viessman et al. 1977).  Viessman et al. (1977) note that, under clear skies, the most significant variables in snowmelt due to radiation are insolation, albedo of snow, and air temperature.  The U.S. Army Corps of Engineers (COE 1956) show that cloud cover and height can significantly affect snowmelt from radiation.  An approximate method of estimating 12-hr depth of snowmelt from direct solar radiation is given by Wilson (1941).  The relationship is of the following form:



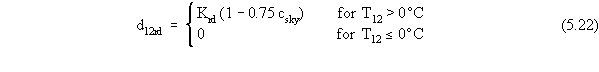
where

d_12rd     is the 12-hr snowmelt from radiation (cm)
K_rd      is the snowmelt occurring by radiation in a half-day in clear weather (cm)
c_sky     is the mean sky cover for a 12-hr period (tenths) (unitless)
T₁₂      is the average 12-hr temperature (^oC).

It is assumed that the 12-hr snowmelt can be extended over the month by using monthly averaged degree of cloudiness.  The monthly estimate of snowmelt from radiation is given by



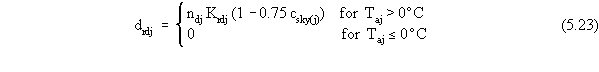
where

d_rdj  is the average monthly snowmelt from radiation for the j-th month (cm)
K_rdj  is the average snowmelt occurring by radiation in a half-day in clear weather for the j-th month (cm).

Viessman et al. (1977) provide estimates of the parameter K_rdj as a function of month (Table 5.7).
 
Table 5.7.  Half-Day Snowmelt During Clear Weather as a Function of Month (after Viessman et al. 1977)

j	Month	Krdj(cm)
3	March	0.89
4	April	1.07
5	May	1.22
6	June	1.33

Rainfall

    Viessman et al. (1977) note that since the temperature of rain falling on a snowpack is probably low, the heat derived from rainfall is generally small.  At higher temperatures, rainfall may constitute a significant heat source; it affects the aging process of the snow, frequently to a great degree.  Based on Viessman et al. (1977) and COE (1960), daily depth of snowmelt by rainfall can be estimated by



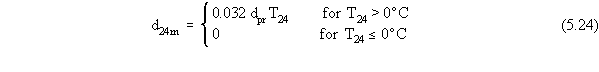
where

d_24rn     is the daily snowmelt during a rainfall event (cm)
d_pr        is the daily precipitation depth (cm)
T₂₄        is the average daily air temperature (^oC).

This equation is applied to the an entire month by assuming that the equation is applicable to each rainfall event during the month, and that the air temperature during each event is the same as the adjusted average monthly temperature.  Computing the depth of snowmelt from rainfall for each precipitation event in the j-th month and summing the results gives the following expression:



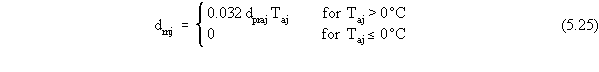
where

d_rnj      is the snowmelt from rainfall for the j-th month (cm)
d_praj     is the precipitation adjusted for snowmelt for the j-th month (cm).

Total Monthly Snowmelt

The total depth of snowmelt on a monthly basis is the sum of the snowmelt depths due to vapor condensation, convection, radiation, and rainfall:



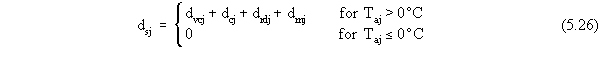
where    d_sj  is the total snowmelt for the j-th month (cm).

The depth of snowmelt is limited by the amount of snow stored on the land surface.  When a month has an adjusted monthly temperature greater than freezing and there is snow stored on the land surface, the monthly precipitation volume is adjusted to account for snowmelt as follows:



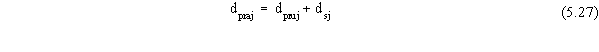
where    d_pruj is the unadjusted precipitation depth for the j-th month obtained from the LCD (cm).

The adjusted precipitation (d_praj) is used to compute net overland runoff and deep-drainage percolation.