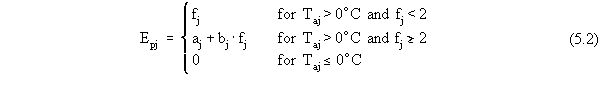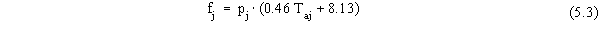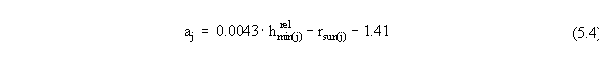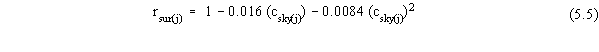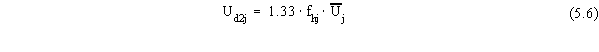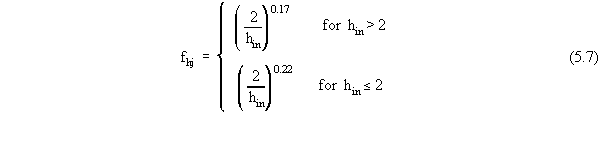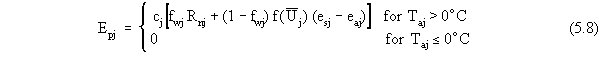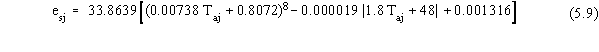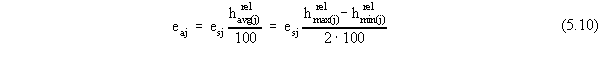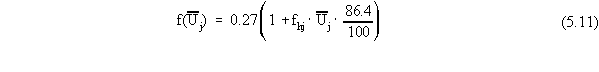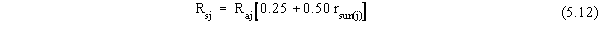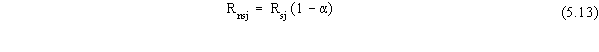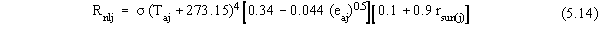5.1.3  Potential Evapotranspiration

Potential evapotranspiration is a critical parameter in the water balance.  If the PET estimate is too high, then the volume of leachate will be underpredicted.  If the PET estimate is too low, then overpredicted leachate-volume estimates may result.  The estimated PET may not be high enough in arid regions, because most of the techniques used for estimating PET were not developed for arid regions.

Rosenberg (1974) notes that the concept of PET has been widely accepted,and he defines it as follows:

"Potential evapotranspiration (PET) is the evaporation from an extended surface of short green . . . (vegetation) . . . which fully shades the ground, exerts little or negligible resistance to the flow of water, and is always well supplied with water.  Potential evapotranspiration cannot exceed free water evaporation under the same weather conditions." (pp. 172)

He further notes that AET differs from PET under most circumstances. He attributes these differences to 1) the influence of surfaces that are not extended (i.e., great fetch), 2) varying heights in vegetation, 3) partial vegetative cover, 4) internal resistance in vegetation to water flow, 5) periodic water deficits (i.e., dry seasons during which vegetation is not well supplied with water), and 6) vegetation using more water in arid and dry regions than that suggested by pan evaporation (i.e., PET exceeding free water evaporation).

Rosenberg (1974) notes that in humid regions (i.e., where advection of sensible heat is unimportant) pan evaporation gives realistic estimates of PET.  In arid localities and where advection is considerable, pan evaporation may give unrealistic values; in fact, he notes that the difference between pan evaporation and PET may be "very pronounced."  In an effort to present a consistent methodology applicable uniformly throughout the country, PET rate is estimated in the module using well-accepted formulations (e.g., the Penman method), as opposed to being assumed equal to pan evaporation rate.

Doorenbos and Pruitt (1977) present four techniques for estimating PET rate:  modified Blaney-Criddle method, Penman method with correction factor, Radiation method, and Pan Evaporation method.  Gee and Simmons (1979) applied three of these techniques (i.e., modified Blaney-Criddle method, Penman method with correction factor, and radiation method) along with the original Penman formulation to the arid Pacific Northwest.  Their results indicate that all methods yielded nearly the same cumulative PET over the 2-year simulation period except for the Penman method, which consistently overpredicted PET.  Of the five methods mentioned above, the modified Blaney-Criddle method, Penman method, and Penman method with correction factor are used in MEPAS.  The modified Blaney-Criddle method was chosen because it was developed for the arid western portions of the United States (Israelsen and Hansen 1962).  The Penman method and Penman method with correction factor were chosen because Doorenbos and Pruitt (1977) believe that they offer the best results with the minimum possible error.  All three methods are applied at each site, and the lowest PET estimate is used in that site's assessment.  Note, this means that the highest estimate of leaching water flux (based on these three methods of PET estimation) is used by the source-term module.  Therefore, because contaminant loss to leaching is maximized (relatively speaking), contaminant loss to other loss routes is correspondingly lower.

The methods used by the source-term release module to estimate PET are described below.  The Penman method and Penman method with correction factor differ only by the correction factor.  Thus, only the modified Blaney-Criddle method and Penman method with correction factor are described in this chapter.

Modified Blaney-Criddle Method

Blaney and Criddle (1950) calculated evapotranspiration from a consumptive-use factor, mean monthly temperature, and percentage of total annual daylight hours occurring during the period being considered (Doorenbos and Pruitt 1977).  An empirically determined consumptive-use crop coefficient was then applied to establish evapotranspiration water requirements.  Israelsen and Hansen (1962) note that this simplified formula was developed for the arid western portion of the United States and provides good estimates of seasonal water needs under these conditions.  Doorenbos and Pruitt (1977) note that the effect of climate is insufficiently defined by considering only temperature and day length, because vegetative water requirements still vary widely among climates that exhibit similar temperatures and day lengths.

 For a better definition of the effect of climate on vegetative requirements, Doorenbos and Pruitt (1977) present a modified version of the Blaney-Criddle technique.  It includes monthly parameters, such as relative humidity, daytime wind speed, ratio of actual to maximum possible sunshine hours, temperature, latitude, and mean daily percentage of total annual daytime hours.

 The method presented by Doorenbos and Pruitt (1977) as adapted for the module is summarized in the following governing equation:



in which



and



where

f_j  is a coefficient for Blaney-Criddle PET function for the j-th month (mm d^-1)
a_j  is a coefficient for Blaney-Criddle PET function for the j-th month (mm d^-1)
b_j  is a coefficient for Blaney-Criddle PET function for the j-th month (unitless)
p_j  is the mean daily percentage of total annual daytime hours as a function of  latitude for the j-th month (unitless)
  is the minimum percent relative humidity for the j-th month (unitless)
r_sun(j) is the ratio of actual to maximum possible sunshine hours for the j-th month (unitless).

The coefficient b_j is a function of minimum relative humidity, ratio of actual to maximum possible sunshine hours, and mean daytime wind speed measured at a 2-m height, and is interpolated from Table 5.1.  The coefficient p_j represents the mean daily percentage of total annual daytime hours and is interpolated from Table 5.2 for a given month and latitude.

In the source term release module, the ratio of actual to maximum possible sunshine hours is estimated from the mean sky cover (i.e., cloudiness) using the following equation (adapted from Doorenbos and Pruitt 1977):



where    c_sky(j) is the mean sky cover for the j-th month obtained from the LCD (tenths) (unitless).

The mean daytime wind speed at a 2-m heightis estimated from the average wind speed for the month.  The ratio between the mean daytime and nighttime wind speeds is approximately 2.  Thus, the mean daytime wind speed corrected to a 2-m measurement height is obtained as follows (adapted from Doorenbos and Pruitt 1977):



in which



where

U_d2j is the mean monthly daytime wind speed at a 2-m height for the j-th month (m s-1)
f_hj  is the factor for the j-th month to correct the wind speed measurement to a 2-m measurement height ( unitless)
is the average wind speed for the j-th month, obtained from the LCD (m s-1)
h_in  is the wind speed measurement height above ground (m).

In many instances, the height of the wind instruments above the ground (h_in) is included on a separate page of the LCD.  If no information is available on h_in, assume 10 m (based on a typical meteorological tower).

Table 5.1.Prediction of b_j Factor for Different Conditions of Minimum Relative Humidity, Sunshine Duration, and Daytime Wind Speed (After Doorenbos and Pruitt 1977)

rsun(j)	(%)
	0	20	40	60	80	100
0 0.2 0.4 0.6 0.8 1.0	0.84 1.03 1.22 1.38 1.54 1.68	0.80 0.95 1.10 1.24 1.37 1.50	0.74 0.87 1.01 1.13 1.25 1.36	0.64 0.76 0.88 0.99 1.09 1.18	0.52 0.63 0.74 0.85 0.94 1.04	0.38 0.48 0.57 0.66 0.75 0.84	Ud2j =0 m/s
0 0.2 0.4 0.6 0.8 1.0	0.97 1.19 1.41 1.60 1.79 1.98	0.90 1.08 1.26 1.42 1.59 1.74	0.81 0.96 1.11 1.25 1.39 1.52	0.68 0.84 0.97 1.09 1.21 1.31	0.54 0.66 0.77 0.89 1.01 1.11	0.40 0.50 0.60 0.70 0.79 0.89	Ud2j =2 m/s
0 0.2 0.4 0.6 0.8 1.0	1.08 1.33 1.56 1.78 2.00 2.19	0.98 1.18 1.38 1.56 1.74 1.90	0.87 1.03 1.19 1.34 1.50 1.64	0.72 0.87 1.02 1.15 1.28 1.39	0.56 0.69 0.82 0.94 1.05 1.16	0.42 0.52 0.62 0.73 0.83 0.92	Ud2j =4 m/s
0 0.2 0.4 0.6 0.8 1.0	1.18 1.44 1.70 1.94 2.18 2.39	1.06 1.27 1.48 1.67 1.86 2.03	0.92 1.10 1.27 1.44 1.59 1.74	0.74 0.91 1.06 1.21 1.34 1.46	0.58 0.72 0.85 0.97 1.09 1.20	0.43 0.54 0.64 0.75 0.85 0.95	Ud2j =6 m/s
0 0.2 0.4 0.6 0.8 1.0	1.26 1.52 1.79 2.05 2.30 2.54	1.11 1.34 1.56 1.76 1.96 2.14	0.96 1.14 1.32 1.49 1.66 1.82	0.76 0.93 1.10 1.25 1.39 1.52	0.60 0.74 0.87 1.00 1.12 1.24	0.44 0.55 0.66 0.77 0.87 0.98	Ud2j =8 m/s
0 0.2 0.4 0.6 0.8 1.0	1.29 1.58 1.86 2.13 2.39 2.63	1.15 1.38 1.61 1.83 2.03 2.22	0.98 1.17 1.36 1.54 1.71 1.86	0.78 0.96 1.13 1.28 1.43 1.56	0.61 0.75 0.89 1.03 1.15 1.27	0.45 0.56 0.68 0.79 0.89 1.00	Ud2j =10 m/s

Table 5.2.  Prediction of p_j Factor for Different Months and Latitudes
                   (After Doorenbos and Pruitt 1977)

	Latitude (degrees)
Month	0	5	10	15	20	25	30	35	40	45	50
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec	0.267 0.269 0.269 0.269 0.271 0.274 0.275 0.274 0.271 0.270 0.269 0.268	0.264 0.268 0.269 0.270 0.273 0.280 0.281 0.278 0.277 0.269 0.267 0.266	0.261 0.266 0.269 0.272 0.276 0.285 0.287 0.282 0.280 0.268 0.264 0.262	0.257 0.264 0.269 0.275 0.281 0.291 0.293 0.287 0.281 0.267 0.260 0.257	0.252 0.261 0.269 0.278 0.287 0.298 0.299 0.291 0.281 0.264 0.254 0.250	0.246 0.257 0.269 0.282 0.294 0.307 0.305 0.295 0.281 0.261 0.247 0.242	0.239 0.253 0.268 0.286 0.303 0.316 0.313 0.300 0.281 0.258 0.240 0.232	0.231 0.248 0.268 0.291 0.312 0.328 0.321 0.304 0.281 0.254 0.231 0.221	0.220 0.243 0.268 0.297 0.322 0.341 0.330 0.309 0.281 0.250 0.222 0.209	0.209 0.236 0.267 0.303 0.334 0.355 0.341 0.315 0.281 0.245 0.211 0.195	0.195 0.228 0.266 0.310 0.346 0.371 0.354 0.322 0.281 0.240 0.200 0.180

 
   Penman Method with Correction Factor  The original Penman method (Penman 1948) is one of the most theoretically based approaches for estimating PET because it is based on incoming solar energy (i.e., radiation) and aerodynamic characteristics (e.g., wind and humidity).  The relative importance of each term varies with climatic conditions.  Doorenbos and Pruitt (1977) note that under calm weather conditions the aerodynamic term is usually less important than the energy term, and the results appear to predict evapotranspiration rather closely.  They continue to note that under windy conditions and particularly in the more arid regions, the aerodynamic term becomes more important; thus, errors may result in predicting PET.  Israelsen and Hansen (1962) appear to concur with Doorenbos and Pruitt (1977) by noting that the coefficients used in the Penman equation: " . . . were determined for a rather humid area not far from the ocean and essentially covered with growing vegetation.  Experience indicates that the Penman formula applies better under these conditions than in arid, low-humidity areas where temperature and radiant energy may not be as nearly balanced as . . . (in a humid area near the ocean)." (pp. 244-245) Doorenbos and Pruitt (1977) developed the modified version of the Penman method, called the Penman method with correction factor.  It differs from the Penman method by using a revised wind function term in its formulation.  The Penman method with correction factor is based on climatic parameters such as maximum, minimum, and mean relative humidity; ratio of actual to maximum possible sunshine hours; average wind speed; average air temperature; saturation and actual vapor pressures; and net shortwave and longwave solar radiation parameters.  The governing PET rate equation in the method is as follows:

where c_j  is the correction factor for the Penman method with correction factor for the j-th month (unitless)
f_wj  is the temperature-related weighting factor for the j-th month (unitless)
R_nj  is the net radiation, in equivalent evaporation, for the j-th month (mm d^-1)
f()  is a wind-related function, explained below
e_aj  is the mean actual vapor pressure of the air for the j-th month (mbar)
e_sj  is the saturation vapor pressure at mean air temperature for the j-th month (mbar). Values for the saturation vapor pressure (e_sj) are given in Table 5.3.  The following equation, proposed by Bosen (1960) and reported by Linsley et al. (1975), is used in the module to estimate the saturation vapor pressure.

(where | • | denotes the absolute value of  • .)
Linsley et al. (1975) note that this equation "yields values of saturation vapor pressure over water that are approximated to within one percent in the range of -50 to +55^o C (-58 to +131^o F)."  Because relative humidity is the percent ratio of the actual vapor pressure to the saturation vapor pressure, the maximum and minimum relative humidities obtained from the LCD are used to find the actual vapor pressure (e_aj) as follows:

where   is the average percent relative humidity for the j-th month (unitless) and
  is the maximum percent relative humidity for the j-th month (unitless).  The temperature-related weighting factor (f_wj) is a function of altitude as well as temperature.  The value for f_wj can be obtained from Table 5.4. The wind-related function is defined in the Penman method with correction factor as

where 86.4 = factor to convert wind speed from m s^-1 to km d^-1.
 


Table 5.3.   Saturated Vapor Pressure Versus Temperature
                                (after Linsley et al. 1975; Doorenbos and Pruitt 1977)

Temperature (oC)	Vapor Pressure (mbar)	Temperature (oC)	Vapor Pressure (mbar)
0	6.1	24	29.8
1	6.6	25	31.7
2	7.1	26	33.6
3	7.6	27	35.7
4	8.1	28	37.8
5	8.7	29	40.1
6	9.3	30	42.4
7	10.0	31	44.9
8	10.7	32	47.6
9	11.5	33	50.3
10	12.3	34	53.2
11	13.1	35	56.2
12	14.0	36	59.4
13	15.0	37	62.8
14	16.1	38	66.3
15	17.0	39	69.9
16	18.2	40	73.8
17	19.4	50	123.4
18	20.6	60	199.3
19	22.0	70	311.7
20	23.4	80	473.7
21	24.9	90	701.1
22	26.4	100	1013.3
23	28.1

Table 5.4.  Values of Weighting Factor (f_wj) for the Effect of Radiation on PET rate at Different Temperatures and Altitudes
(after Doorenbos and Pruitt 1977)

	Temperature(EC)
Altitude (m)	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36	38	40
0	0.43	0.46	0.49	0.52	0.55	0.58	0.61	0.64	0.66	0.69	0.71	0.73	0.75	0.77	0.78	0.80	0.82	0.83	0.84	0.85
500	0.44	0.48	.051	0.54	0.57	0.60	0.62	0.65	0.67	0.70	0.72	0.74	0.76	0.78	0.79	0.81	0.82	0.84	0.85	0.86
1000	0.46	0.49	0.52	0.55	0.58	0.61	0.64	0.66	0.69	0.71	0.73	0.75	0.77	0.79	0.80	0.82	0.83	0.85	0.86	0.87
2000	0.49	0.52	0.55	0.58	0.61	0.64	0.66	0.69	0.71	0.73	0.75	0.77	0.79	0.81	0.82	0.84	0.85	0.86	0.87	0.88
3000	0.52	0.55	0.58	0.61	0.64	0.66	0.69	0.71	0.73	0.75	0.77	0.79	0.81	0.82	0.84	0.85	0.86	0.87	0.88	0.89
4000	0.54	0.58	0.61	0.64	0.66	0.69	0.71	0.73	0.75	0.77	0.79	0.81	0.82	0.84	0.85	0.86	0.87	0.89	0.90	0.90

 
 
The total net radiation (R_nj) is equal to the difference between the net shortwave radiation (R_nsj) and the net longwave radiation (R_nlj).  When converted to heat, R_nj can be related to the energy (i.e., extraterrestrial radiation [R_aj]) required to evaporate water from an open surface (Doorenbos and Pruitt 1977).  To calculate R_nj, the following steps are involved:

•    Determine Raj using Table 5.5 based on latitude (provided in the LCD) and month of year.

Table 5.5.   Extraterrestrial Radiation (R_aj) for the Northern Hemisphere Expressed in
           Equivalent Evaporation (mm d^-1) (after Doorenbos and Pruitt 1977)

Latitude	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
50E	3.8	6.1	9.4	12.7	15.8	17.1	16.4	14.1	10.9	7.4	4.5	3.2
48	4.3	6.6	9.8	13.0	15.9	17.2	16.5	14.3	11.2	7.8	5.0	3.7
46	4.9	7.1	10.2	13.3	16.0	17.2	16.6	14.5	11.5	8.3	5.5	4.3
44	5.3	7.6	10.6	13.7	16.1	17.2	16.6	14.7	11.9	8.7	6.0	4.7
42	5.9	8.1	11.0	14.0	16.2	17.3	16.7	15.0	12.2	9.1	6.5	5.2
40	6.4	8.6	11.4	14.3	16.4	17.3	16.7	15.2	12.5	9.6	7.0	5.7
38	6.9	9.0	11.8	14.5	16.4	17.2	16.7	15.3	12.8	10.0	7.5	6.1
36	7.4	9.4	12.1	14.7	16.4	17.2	16.7	15.4	13.1	10.6	8.0	6.6
34	7.9	9.8	12.4	14.8	16.5	17.1	16.8	15.5	13.4	10.8	8.5	7.2
32	8.3	10.2	12.8	15.0	16.5	17.0	16.8	15.6	13.6	11.2	9.0	7.8
30	8.8	10.7	13.1	15.2	16.5	17.0	16.8	15.7	13.9	11.6	9.5	8.3
28	9.3	11.1	13.4	15.3	16.5	16.8	16.7	15.7	14.1	12.0	9.9	8.8
26	9.8	11.5	13.7	15.3	16.4	16.7	16.6	15.7	14.3	12.3	10.3	9.3
24	10.2	11.9	13.9	15.4	16.4	16.6	16.5	15.8	14.5	12.6	10.7	9.7
22	10.7	12.3	14.2	15.5	16.3	16.4	16.4	15.8	14.6	13.0	11.1	10.2
20	11.2	12.7	14.4	15.6	16.3	16.4	16.3	15.9	14.8	13.3	11.6	10.7
18	11.6	13.0	14.6	15.6	16.1	16.1	16.1	15.8	14.9	13.6	12.0	11.1
16	12.0	13.3	14.7	15.6	16.0	15.9	15.9	15.7	15.0	13.9	12.4	11.6
14	12.4	13.6	14.9	15.7	15.8	15.7	15.7	15.7	15.1	14.1	12.8	12.0
12	12.8	13.9	15.1	15.7	15.7	15.5	15.5	15.6	15.2	14.4	13.3	12.5
10	13.2	14.2	15.3	15.7	15.5	15.3	15.3	15.5	15.3	14.7	13.6	12.9
8	13.6	14.5	15.3	15.6	15.3	15.0	15.1	15.4	15.3	14.8	13.9	13.3
6	13.9	14.8	15.4	15.4	15.1	14.7	14.9	15.2	15.3	15.0	14.2	13.7
4	14.3	15.0	15.5	15.5	14.9	14.4	14.6	15.1	15.3	15.1	14.5	14.1
2	14.7	15.3	15.6	15.3	14.6	14.2	14.3	14.9	15.3	15.3	14.8	14.4
0	15.0	15.5	15.7	15.3	14.4	13.9	14.1	14.8	15.3	15.4	15.1	14.8

• Compute the solar radiation (R_sj) by correcting R_aj for the ratio of the actual to the maximum possible sunshine hours (r_sun(j), percentage of possible sunshine in the LCD, or estimated from Equation 5.5).

where R_sj  is the solar radiation, in equivalent evaporation, for the j-th month (mm d^-1)
R_aj  is the extraterrestrial radiation, in equivalent evaporation for the j-th month (mm d^-1).

•     Compute R_nsj by correcting R_sj for the reflectiveness of the land surface (Doorenbos and Pruitt 1977):

 where R_nsj  is the net shortwave radiation, in equivalent evaporation, for the j-th month (mm d^-1) a is the land surface reflectiveness correction parameter (unitless=0.25).

• R_nlj is estimated based on the average temperature, the actual vapor pressure (e_aj), and the ratio of actual to maximum possible sunshine hours r_sun(j) as follows:

where R_nlj  is the net longwave radiation, in equivalent evaporation, for the j-th month  (mm d^-1)
s is a constant in the estimation equation for R_nlj (unitless=2.0x10^-9)
273.15 = unit conversion from  ^oC to K

•     Compute R_nj as the algebraic difference between R_nsj and R_nlj:

The correction factor (c_j) which compensates for the effects of day and night weather conditions, can be estimated from , R_sj, and .  By assuming that the ratio of the daytime to nighttime average wind speeds is equal to 2 (see Section 5.1.3.1), the factor c_j can be estimated from Table 5.6.
 


Table 5.6.   Adjustment Factor (c_j) in the Penman Method with Correction Factor Equation
(After Doorenbos and Pruitt 1977)

Rsj (mm/d) Uj (m/s)	= 30%				= 60%				= 90%
	3	6	9	12	3	6	9	12	3	6	9	12
0	0.86	0.90	1.00	1.00	0.96	0.98	1.05	1.05	1.02	1.06	1.10	1.10
3	0.69	0.76	0.85	0.92	0.83	0.91	0.99	1.05	0.89	0.98	1.10	1.14
6	0.53	0.61	0.74	0.84	0.70	0.80	0.94	1.02	0.79	0.92	1.05	1.12
9	0.37	0.48	0.65	0.76	0.59	0.70	0.84	0.95	0.71	0.81	0.96	1.06

 
 

---