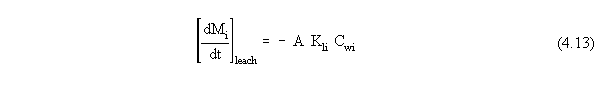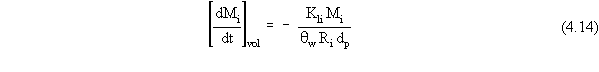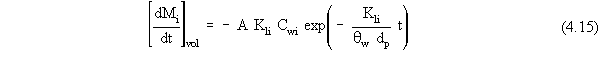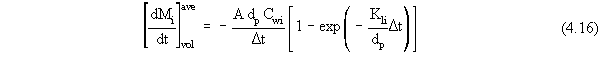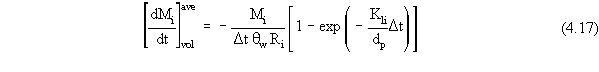4.1.4 Volatilization
It is assumed that contaminants in the pond/surface impoundment volatilize
into the atmosphere above the pond only from the aqueous phase (i.e., no
contaminants volatilize directly from the surface of suspended sediment
particles or NAPL-phase globules that may be located at the surface of
the pond and that may periodically be in contact with the atmosphere).
This seems to be a reasonable assumption because the vast majority of the
pond surface should be an air-water interface rather than a sediment-air
or globule-air interface. With this assumption, and the fact that
the contaminants are assumed to be dilute constituents of the aqueous phase,
standard theory (USEPA 1988a, 1990) for volatilization from the surface
of a water body should apply. This theory is based on the "two-resistance"
model (Thibodeaux 1979; Hwang 1982; Mackay and Leinonen 1975) which assumes
that the controlling mechanisms for volatilization from the bulk solution
to the atmosphere are the diffusion resistances of thin transition layers
in the liquid phase and the gas phase located at the air-water interface.
Based on this theory, the mass flux equation for loss from the pond/surface
impoundment by volatilization (either alone or simultaneous with the other
processes) can be expressed as
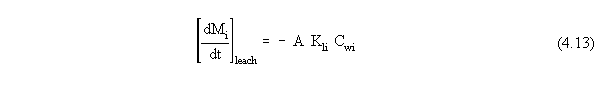
where Kli is the overall mass transfer coefficient from a liquid
phase to the atmosphere for contaminant i, expressed in terms of
the liquid-phase concentration (cm yr-1).
When suspended globules of a NAPL phase exist in the pond, the aqueous
concentration of the contaminant is controlled by the composition of the
NAPL phase. In this case, the source-term release module calculates
the value of Cwi in Equation 4.13 by the phase partitioning
theory described in Section 2.2.4 (which uses different methods, depending
on the mole fraction [or concentration] of the contaminant in the NAPL
phase).
When no suspended globules of a NAPL phase exist in the pond,
the aqueous concentration can be calculated by a simple phase partitioning
relation (i.e., Equation 4.9). Now, substituting Equation 4.9 into
Equation 4.13, the mass flux equation for contaminant loss (when no NAPL
is present) from the pond/surface impoundment by volatilization (either
alone or simultaneous with the other processes) can be expressed as
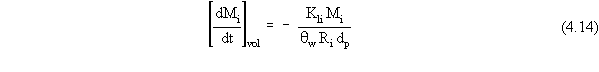
The expressions in Equations 4.13 and 4.14 represent instantaneous
rates of mass loss at a specific time (just like the expressions for all
other mass loss term presented thus far). However, during the course
of testing the source-term release module, it was discovered that for certain
more volatile compounds, these expressions caused all of the initial contaminant
inventory to be lost to volatilization in the firsttime step (which was
1 yr for those runs). It was hypothesized that the reason for this
was that a 1-yr time step was too large for the Runge-Kutta numerical solution
for volatilization. However, applications of RAAS/MEPAS often simulate
scenarios that cover an extremely long time period (e.g., 10,000 yr).
So, using a time step significantly smaller than 1 yr would cause undesirably
long run times. In addition, modifying the numerical solution algorithm
to use variable-length time steps, the size of which would be determined
by limits on the magnitude of contaminant mass that could be lost in any
given time step, was deemed beyond the scope of the current version of
the source-term release module.
The approach taken to compensate for these high volatilization
loss predictions was to use a mass loss expression that was time-averaged
over the time step (rather than instantaneous). This will reduce
the predicted flux because the time-averaged expression accounts for the
fact that the flux decreases over time as the aqueous concentration decreases.
One simplifying assumption made is that the time-averaged formula for volatilization
loss can be derived by assuming that volatilization is the only process
contributing to loss over the time step. Another simplifying assumption
made is that aqueous contaminant is not replenished by desorption from
suspended sediment or dissolution from the NAPL phase as it is decreased
through volatilization. This latter assumption must be made because
the complex phase partitioning theory required when a NAPL phase is present
precludes deriving an analytical expression for the time-averaged mass
loss.
Mackay and Leinonen (1975) began with an expression similar to
Equation 4.13, and derived a transient-state expression for volatilization
from a pond where only aqueous contaminant is present that was applicable
for times t = 0 to t = t. . The analogous transient-state expression
applicable for times between the beginning and end of a time step (of size
Dt), is
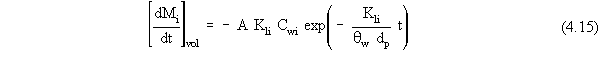
In Equation 4.15, Cwi should be interpreted as the concentration
at the beginning of the time step, and t should be interpreted as the length
of time from the beginning of the time step. As stated above, if
we assume that only aqueous mass changes during the time step, Equation
4.15 can be averaged over the time step to obtain
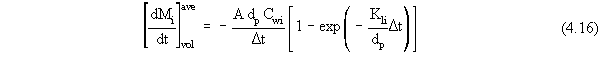
Note that when Kli is small, Equation 4.16 reduces to Equation
4.13; which means that using Equation 4.16 for compounds that are not highly
volatile (for which there was no problem with the instantaneous mass loss
expressions) is equivalent to using the instantaneous mass loss expressions.
So, when suspended globules of a NAPL phase exist in the pond, the module
actually uses Equation 4.16, coupled with phase partitioning theory to
determine Cwi. When no suspended globules of a NAPL phase
exist in the pond, the module actually uses
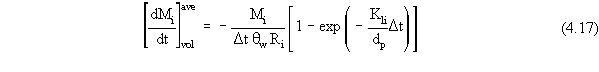
which is the analogue of Equation 4.14 (and reduces to it when Kli
is small [or, more precisely, when the argument of the exponential function
on the right-hand side of Equation 4.17 is small]).