4.1.2  Leaching

The leaching process is assumed to occur by advective transport of the aqueous contaminant out of the bottom face of the pond along with the infiltrating pond water (i.e., no contaminated suspended sediment or NAPL-phase globules leach).  This means that the rate of loss of mass at any given time isgiven by the volumetric flux of water out of the source zone face multiplied by the aqueous concentration of the contaminant in the water at that time:^(a)



The volumetric water flux, in turn, can be expressed in terms of the Darcy water flux density (i.e., Darcy velocity) of the infiltrating water and the area of the bottom face of the source zone:



By substituting Equation 4.7 in Equation 4.6, the mass flux equation for loss from the source zone by leaching can be expressed as



Again, this equation applies if leaching is the only loss process, and also if the other processes are occurring simultaneously.

 When suspended globules of a NAPL phase exist in the pond, the aqueous concentration of the contaminant is controlled by the composition of the NAPL phase.  In this case, the source-term release module calculates the value of C_wi in Equation 4.8 by the phase partitioning theory described in Section 2.2.4 (which uses different methods, depending on the mole fraction [or concentration] of the contaminant in the NAPL phase).

 When no suspended globules of a NAPL phase exist in the pond, the aqueous concentration can be calculated by a simple phase partitioning relation (i.e., Equation 2.7 in Section 2.2.3).  Substituting Equation 4.1 into Equation 2.7, the aqueous concentration can be given by



Now, substituting Equation 4.9 into Equation 4.8, the mass flux equation for loss from the source zone by leaching (when no NAPL is present) can be expressed as



Recall that the phase apportionment factor, R_i, that appears in Equation 4.10 was defined in general terms by Equation 2.5.  It is worthwhile to note that for the contaminated pond/surface impoundment source zone, the "volumetric water content" will be very close to one, and solid-sorbent bulk density in Equation 2.5 is equal to the suspended sediment concentration, ß_ss.

---

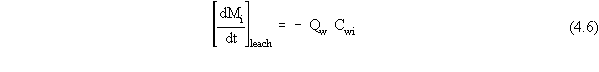
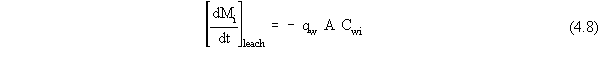
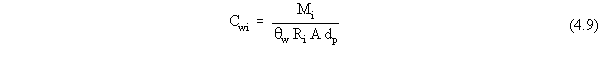
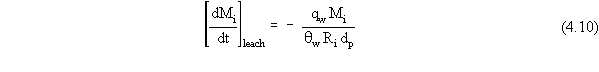
(a)

Note that, in a strict sense, the variable Qw should really be referred to as the aqueous solution flux (which contains water and dissolved constituents). However, because aqueous solutions are typically volumetrically dilute with respect to their dissolved constituents, it is quite common to refer to the aqueous solution flux as the water flux.