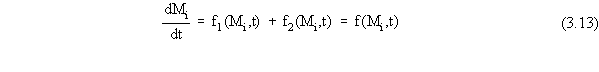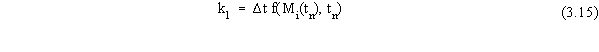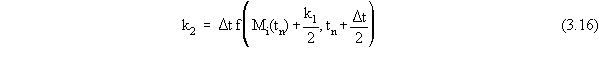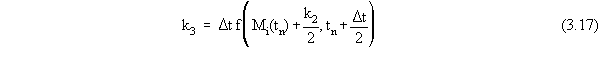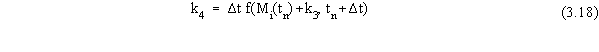3.3 Numerical Solution Procedure for the General Case

In the general case of multiple, concurrent, contaminant loss routes, an analytical solution to Equation 3.4 is not always possible for the following reasons.  Firstly, if a NAPL phase is present in the source zone, the leaching term cannot be expressed as a single, simple function of M_i and t.  Secondly, even if a NAPL phase did not exist, the leaching term may be an arbitrary function of time.  By this we mean that the Darcy water flux density in the aquifer (for the scenario under study) may vary in time due to natural phenomena or the implementation of remediation methodologies.  The user has the ability to enter the Darcy water flux density in the aquifer as a time series of discrete values.  There are no hard limits on the number of elements constituting the time series used to describe such a parameter.  The code will allocate available memory as it is needed.  Therefore any arbitrary transient Darcy water velocity can be accommodated, provided memory and run time limits are not exceeded.  Equation 3.4 can be represented by the general form:



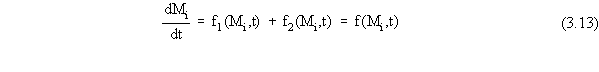
where    f(•), f₁(•), and f₂(•) are generic representation of functions.

The source-term release module solves this first-order, ordinary differential equation numerically by using a fourth-order Runge-Kutta method.  This method requires four computations of the function f(•) for each time step (Dt).  However, one of the benefits of this method over other methods is that a larger time step can be used while keeping the error below some desired level.  This method has an accumulated error on the order of (Dt).  This means that if you cut the time step in half, you decrease the error by a factor of 16.  In comparison, if Euler's method was used, cutting the time step in half would only decrease the error by a factor of 2.  The Runge-Kutta method can therefore use a much larger time step than the Euler method, which will more than compensate for the extra computations required per time step.

 The numerical solution algorithm begins at time t = 0 with M_i = M_io.  The Runge-Kutta algorithm for updating contaminant mass over the course of a time step is given by



where the terms in Equation 3.14 are given by









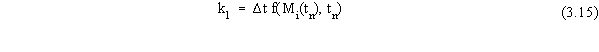
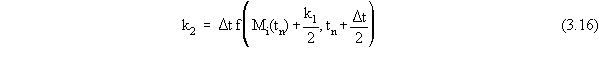
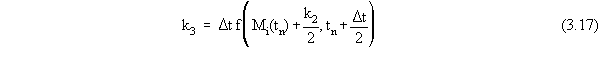
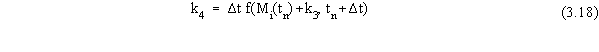
where    M_i(t_n) is the value of Mi at time nDt, and t_n is the time nDt.

The value of M_i is therefore updated in a stepwise fashion over finite intervals of time.

 Note that because the function f(•) can be expressed as the sum of the functions f₁(•) and f₂(•) (from Equation 3.13), the Runge-Kutta procedure used to update the total contaminant mass in the source zone (described in Equations 3.14 - 3.18) contains calculations of the k₁ through k₄ terms that would be associated with the individual functions f₁(•) and f₂(•).  Because these functions are associated with the individual mass loss terms, the numerical scheme allows us to also obtain the individual mass fluxes to each loss route at discrete times with minimal extra computation.  This entire procedure is repeated as long as not all of the contaminant mass has been depleted from the source zone.