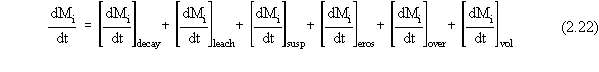2.3 General Form of Contaminant Loss Rate Expressions

In general, the mass (or activity) of contaminant i in the source zone decreases over time because the contaminant is being removed from the zone by a number of different processes.  The processes considered by the source-term release module are first-order decay/degradation, leaching to the vadose zone or groundwater, wind suspension of contaminated surface soil particles, water erosion of contaminated surface soil particles, overland flow of contaminated water from the source, and volatilization from the source into the atmosphere.  The overall rate of change of contaminant mass in the source zone can be related to the mass loss rates (i.e., mass fluxes) to each loss route by the following general differential equation:



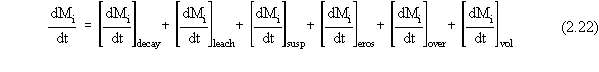
where    t is the time since initial condition of the source zone. (yr)

For each type of contaminated source zone, each mass flux term on the right-hand side of Equation 2.22 must either be set identically to zero (if that particular loss process does not apply to that type of source zone) or defined by appropriate theoretical expressions derived from the physics and chemistry of the loss processes.  When multiple processes occur simultaneously, they can interact.  This synergistic or antagonistic process interaction can cause the mathematical expression for a given term in Equation 2.22 to be different from what it would be if that process was the only one removing mass from the source zone.  The explicit forms of these terms are derived in the report sections related to each type of source zone (Sections 3.0, 4.0, and 5.0).

 Once the right-hand side of Equation 2.22 is expressed as a function of contaminant mass and time, the resulting first-order, ordinary differential equation can be solved by standard numerical methods to update the contaminant mass at discrete time intervals.  (Note that for the contaminated vadose zone source zone, an additional differential equation must be solved simultaneously.)  The individual terms on the right-hand side of Equation 2.22 (which can also be expressed as first-order, ordinary differential equations) are solved numerically as part of the overall numerical solution of Equation 2.22.  The results of the calculations for the individual terms are used to produce the mass loss fluxes to each loss route at discrete time intervals.  Because the behavior of some contaminants is linked with that of other contaminants (i.e., those present in a NAPL phase), the masses and loss fluxes of all contaminants are updated within a single time step before the module proceeds to calculations for the next time step.