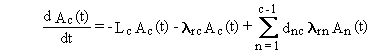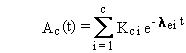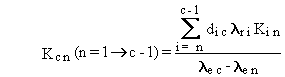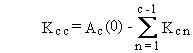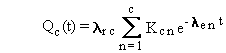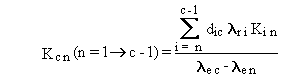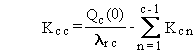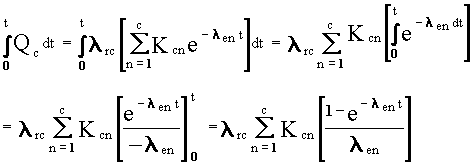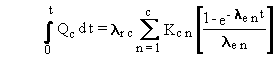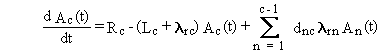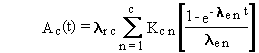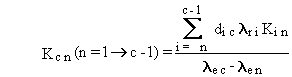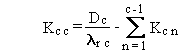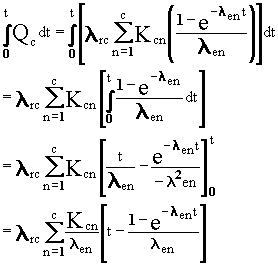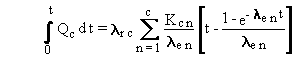APPENDIX B
RADIONCULIDE DECAY ALGORITHMS


    A general solution to first-order compartmental models is presented in this appendix for application to systems consisting of one physical medium that contains any number of radionuclide decay chain members. The solution can be applied to any such system involving physical transfers from the medium and radioactive chain decay with branching. The general analytical solution to the problem is described mathematically. The general analytical solution is extended to evaluation of the time integral of the radionuclide quantities and to cases involving deposition from outside sources. For deposition at a constant rate during a time period, the general solution can be applied to determine the quantity present during the time period and the time integral of the quantity during the time period.

    Various methods have been described for evaluating systems involving radioactive decay (Bateman 1910; Friedlander and Kennedy 1955; Hamawi 1971; Scherpelz and Desrosiers 1980) and physical transfers between media (Gear 1971; Skrable et al. 1974; Hindmarsh 1983; Birchall and James 1989; Kirchner 1990). Some of these methods involve simple analytical solutions, such as the Bateman (1910) representation of the radioactive decay process without branching; others involve advanced numerical methods to solve multi-compartment system such as the numerical differential equation solvers of Gear (1971) and Hindmarsh (1983) and the numerical matrix method described by Birchall and James (1989). The analytical solutions presented by Bateman (1910), Scherpelz and Desrosiers (1980), and Skrable et al. (1974) do not consider branching, but can account for branching by performing multiple applications of the equations to each possible decay path and summing the results appropriately, a method suggested by Friedlander and Kennedy (1955). The general solution presented in this appendix includes chain decay with branching explicitly in the equations (Kennedy and Strenge 1992).

    The general radioactive-decay-chain problem is illustrated in Figure B.1. In this figure each box represents a radionuclide decay chain member in a medium. Two types of transfers may be represented: radioactive decay between chain members and physical transfer from the medium. Radioactive transitions in this system are represented as flowing from upper boxes to lower boxes; any upper box may contribute material to any lower box. Because radioactive transitions within decay chains are irreversible, upward transfers, representing recycling of material, are not considered. Physical transfers out of the medium are indicated by the downward arrows from each box.

    This appendix presents four applications of the general solution for the compartmental system of Figure B.1. First, the solution is presented for the evaluation of the quantity of radionuclides in each box as a function of time, based on a user-defined initial inventory. The general solution is presented


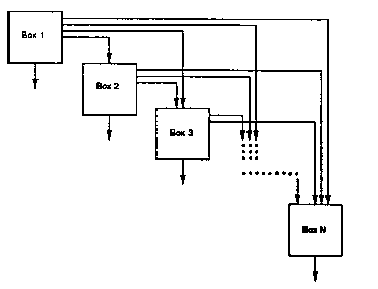
FIGURE B.1 A Representation of the General Radioactive-Decay-Chain Problem


for quantities expressed in units of atoms and activity. The solution then is extended for use to evaluate three additional situations. The first extension covers the evaluation of the time integral of the quantity in each box during a time period. The general solution also is shown to apply to cases involving deposition of radionuclides at a constant rate to a medium when the initial quantity in each box is zero. This application provides the quantity in each box after accumulation during a time period, and can be extended to provide the time integral of the quantity of each chain member from deposition accumulation during a time period.

General Solution

    An algorithm for evaluations using the general solution equations is given to demonstrate translation of the method to computer applications. In the system of boxes as shown in Figure B.1, each box may involve 1) transfer to any other box lower in the system and 2) loss by radioactive decay within each box with generation of progeny in a lower box. Transfers between boxes are described by rate constants. The general differential equation for the change in the quantity of a radionuclide in the medium is described by the following word equation:

(Rate of change of chain member c) =
Radioactive transitions of precursor radionuclides are represented in the last term.

The equivalent mathematical form of this equation is as follows.

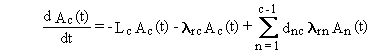
(B.1)



where
    The first term on the right side of Equation (B.1) represents physical transfers of chain member c out of the medium. The rate constant, Lc, is the sum of all physical transfer rate constants from the media (for chain member c). The second term represents loss by radioactive transitions of the radionuclide of chain member c to progeny radionuclides in other boxes. The last term represents production of the chain member c from all precursor radionuclides.

The general solution can be summarized by the following four equations.

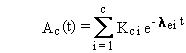
(B.2)



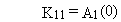
(B.3)



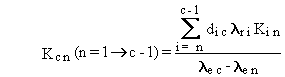
(B.4)



and

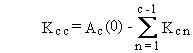
(B.5)



    The previous discussion and equations describe quantities of radionuclides expressed in units of atoms. Equations (B.2) through (B.5) can be easily converted to units of activity, such as Bq or Ci, using the general relationship between atom and activity units:

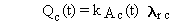
(B.6)



where
and Ac(t) is as previously defined. When activity is expressed in Bq and time in seconds, the constant equals 1.

    Substituting the expression in Equation (B.6) into Equations (B.2) through (B.5), with the terms slightly simplified, results in the following general solution with quantities expressed in activity units:

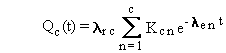
(B.7)



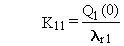
(B.8)



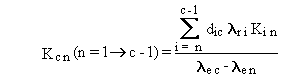
(B.9)



and

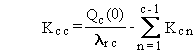
(B.10)



    The forms of Equations (B.7) through (B.10) suggest some limitations on definition of numerical values for rate constants. First, all boxes must represent a radioactive material, because the radioactive-transition rate constant appears in the denominator of Equations (B.8) and (B.10). Stable elements at the end of a decay chain can be simulated as a material with a long but finite radioactive half-life. This limitation does not apply to the general solution expressed in atom units, Equations (B.2) through (B.5), although a stable progeny will effectively terminate a radioactive decay chain, because the rate constant for a stable isotope is zero. Another limitation is that the effective rate constant for any two boxes, lec and len, must not be equal, because their difference appears in the denominator of Equations (B.4) and (B.9). This limitation applies only to pairs of chain members that have radioactive transfers from one to the other.

    Use of the general solution given here requires definition of all rate constants and branching fractions. Data on radionuclide half-lives, decay chains, and fractional branching within chains has been published by Lederer and Shirley (1978) and the International Commission on Radiological Protection in ICRP Publication 38 (ICRP 1983).

Extension to Time-Integration

    The discussions and equations to this point have centered on evaluation of the quantity of radionuclides present as a function of time. The general solution can be extended easily to provide the time integral of the quantity present during a time period. This extension is demonstrated by observing that the general solution includes the time variable, t, only in the exponential term of Equations (B.2) and (B.7). Obtaining the time-integral expression involves simply integrating the exponential expression and evaluating the integral from time zero to the desired time. The following sequence applied to Equation (B.7) illustrates these steps:

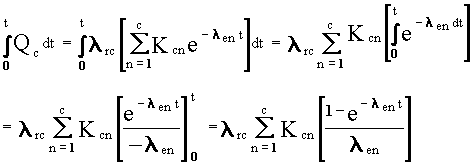
(B.11)



The general solution for the time integral now uses the following formula with Equations (B.8), (B.9), and (B.10):

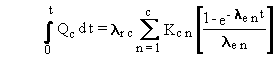
(B.12)



Extension to Deposition at a Constant Rate

    Another extension of the general solution applies to deposition of radionuclides to a medium and accumulation during a time period. The extension assumes that there are initially no radionuclides in the medium. The differential equation for chain member c, is based on Equation (B.1), with an added term representing the constant rate of deposition of chain member c to the medium, Rc.

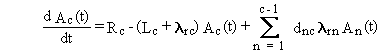
(B.13)



where    Rc = constant deposition rate of chain member c to the medium (atoms/d) and other terms are as previously defined. The general solution to this problem is written as follows, with quantities expressed in activity units:

            

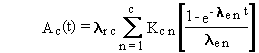
(B.14)



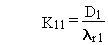
(B.15)



            

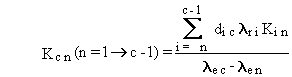
(B.16)



and

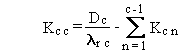
(B.17)



where    Dc is the constant deposition rate of chain member c expressed in terms of activity (pCi/d), and other terms are as previously defined.

    This solution is identical to that for the time-integral problem except for substitution of Dc for Qc(0), and the integral of the exponential for the exponential as illustrated in Equations (B.11) and (B.12).

Extension to Deposition with Time-Integral

    The equations for deposition at a constant rate with accumulation can be integrated to give the time integral of the quantities in each box during a time period. This integration, similar to that described in Equation (B.11), works as follows:

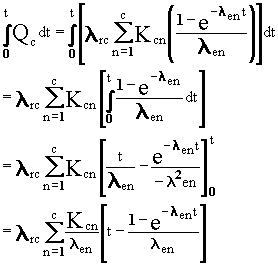
(B.18)



or

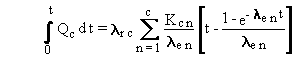
(B.19)



    The general solution to the time integral of deposition at a constant rate with accumulation uses Equation (B.19) [in place of Equation (B.14)], and Equations (B.15), (B.16), and (B.17). These equations can be put in terms of atom units by using Equation (B.6), as illustrated earlier.


REFERENCES

Bateman, H. 1910. "Solution of a System of Differential Equations Occurring in The Theory of Radio-Active Transformation." Proc. Cambridge Phil. Soc. 15:423-427.

Birchall, A., and A. C. James. 1989. "A Microcomputer Algorithm for Solving First Order Compartmental Models Involving Recycling." Health Phy. 56(6):857-868.

Friedlander, G., and J. W. Kennedy. 1955. Nuclear and Radiochemistry. John Wiley & Sons, New York.

Gear, C. W. 1971. Numerical Initial Value Problems in Ordinary Differential Equations, pp 158-166. Prentice-Hall, Englewood Cliffs, New Jersey.

Hamawi, J. M. 1971. "A Useful Recurrence Formula for the Equations of Radioactive Decay." Nucl. Tech. 11:84-88.

Hindmarsh, A. C. 1983. "Toward a Systemized Collection of ODE Solvers." Scientific Computing, ed. R. S. Stepleman. 10th IMACS World Congress on Systems Simulation and Scientific Computation, North-Holland Publishing Company, Amsterdam, The Netherlands.

ICRP (International Commission on Radiological Protection). 1983. Radionuclide Transformations - Energy and Intensity of Emissions, Vol. 11-13, ICRP Publication 38, Pergamon Press, New York.

Kennedy, W. E., Jr., and D. L. Strenge. 1992. Residual Radioactive Contamination from Decommissioning: Technical Basis for Translating Contamination Levels to Annual Total Effective Dose Equivalent, Vol. 1. NUREG/CR-5512, (PNL-7994), U.S. Nuclear Regulatory Commission, Washington, D.C.

Kirchner, T. B. 1990. TIME-ZERO The Integrated Modeling Environment: Reference Manual. Quaternary Software, Inc., Fort Collins, Colorado.

Lederer, C. M., and V. S. Shirley. 1978. Table of Isotopes, 7th ed. John Wiley & Sons, Inc., New York.

Scherpelz, R. Il, and A. E. Desrosiers. 1980. "A Modification to a Recurrence Formula for Linear First-Order Equations." Health Phy. 40:905-907.

Skrable, K., C. French., G. Chabot, and A. Hajor. 1974. "A General Equation for the Kinetics of Linear First Order Phenomena and Suggested Applications." Health Phy. 27:155-57.